问题1005: Let a, b, c be positive real numbers such that a b c=1. Show that if
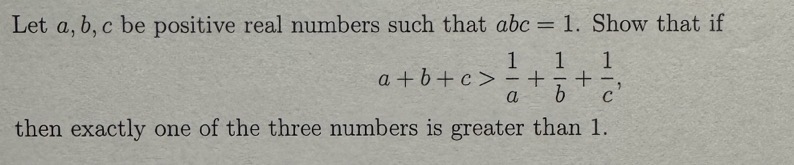
Let $a, b, c$ be positive real numbers such that $a b c=1$. Show that if
$$ a+b+c>\frac{1}{a}+\frac{1}{b}+\frac{1}{c} $$
then exactly one of the three numbers is greater than 1 .
急！！！谢谢！！！
可以更快获取解答
∵abc=1,a>0,b>0,c>0
不妨设：a≥b≥c>0
∴a>1,c<1
将abc=1代入原式可得：
a+b+c>ab+bc+ac
∴a+b+c-ab-bc-ac>0
∴abc-ab-ac-bc+a+b+c-1>0 【abc=1,上式加上abc再减1值不变】
∴(a-1)(b-1)(c-1)>0
且a-1>0,c-1<0
∴b-1>0
∴b>1