问题1692: The area of the uniform cross section of a prism
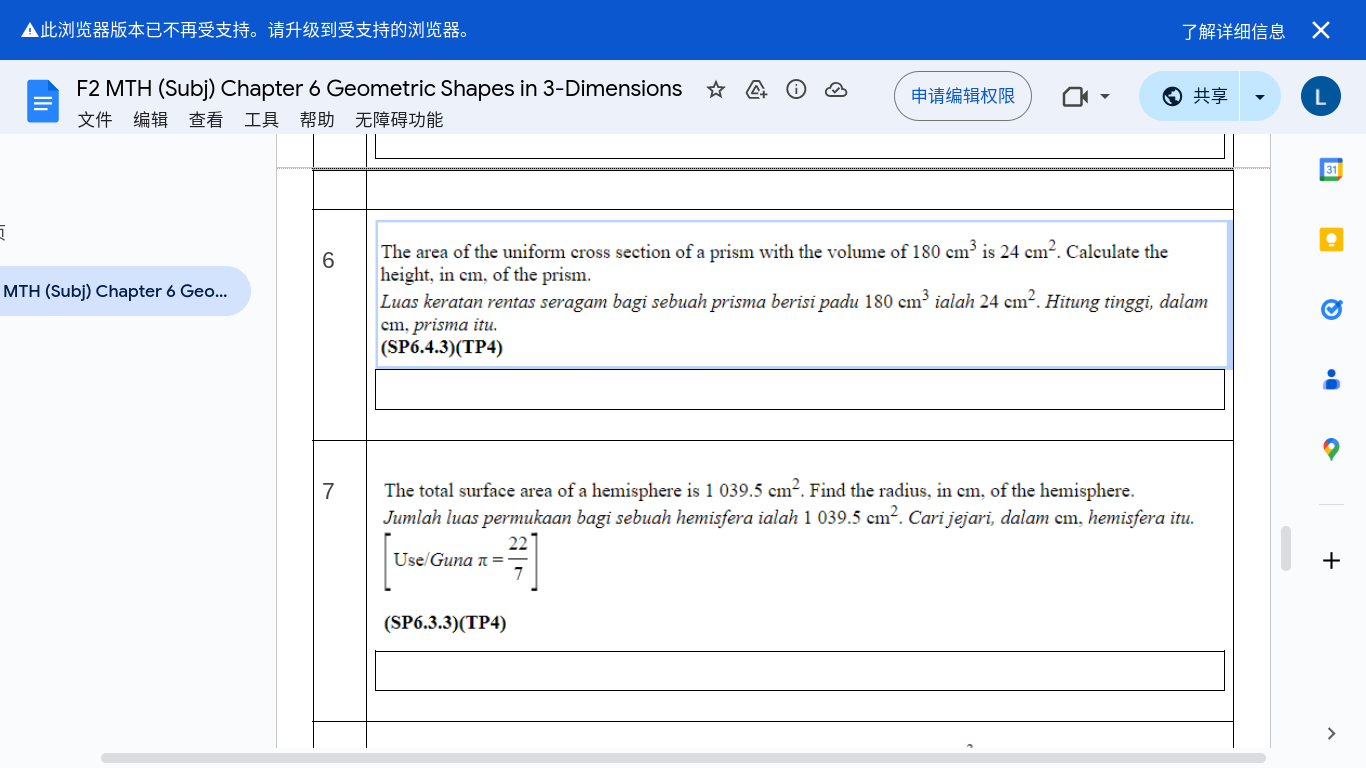
The area of the uniform cross section of a prism with the volume of 180 em^3 is 24 cm. Calculate the height, in cm, of the prism.
Let's solve the problem step by step.
Given:
We need to find the height \( h \) of the prism.
The formula for the volume of a prism is:
\[
V = A \times h
\]
where:
We can rearrange this formula to solve for \( h \):
\[
h = \frac{V}{A}
\]
Now, substitute the given values:
\[
h = \frac{180}{24}
\]
Calculate the division:
\[
h = 7.5
\]
Therefore, the height of the prism is \( 7.5 \text{cm} \).
\[
\boxed{7.5}
\]
添加微信 可以更快获取解答
可以更快获取解答
最后修改于2025年08月20日
前一篇:问题1691: 日期计算
下一篇:问题1695: (3)在菱形ABCD中,CA=120°,AB=3V2.若点P在射线CD