问题1710: 动点问题

在平面直角坐标系中,抛物线 \( y = ax^2 + bx + 3 \)(\( a \neq 0 \))经过 \( A(-1, 0) \),\( B(3, 0) \) 两点,与 \( y \) 轴交于点 \( C \),\( P \) 是抛物线上一动点,且在直线 \( BC \) 的上方。
(1) 求抛物线的解析式;
(2) 如图,连接 \( AC, PC, AP \),\( AP \) 与 \( BC \) 交于点 \( G \),过点 \( P \) 作 \( PF \parallel AC \) 交 \( BC \) 于点 \( F \)。记 \( \triangle ACG \)、\( \triangle PCG \)、\( \triangle PGF \) 的面积分别为 \( S_1 \)、\( S_2 \)、\( S_3 \)。当 \( \dfrac{S_3}{S_2} + \dfrac{S_2}{S_1} \) 取得最大值时,求 \( \sin \angle BCP \) 的值。
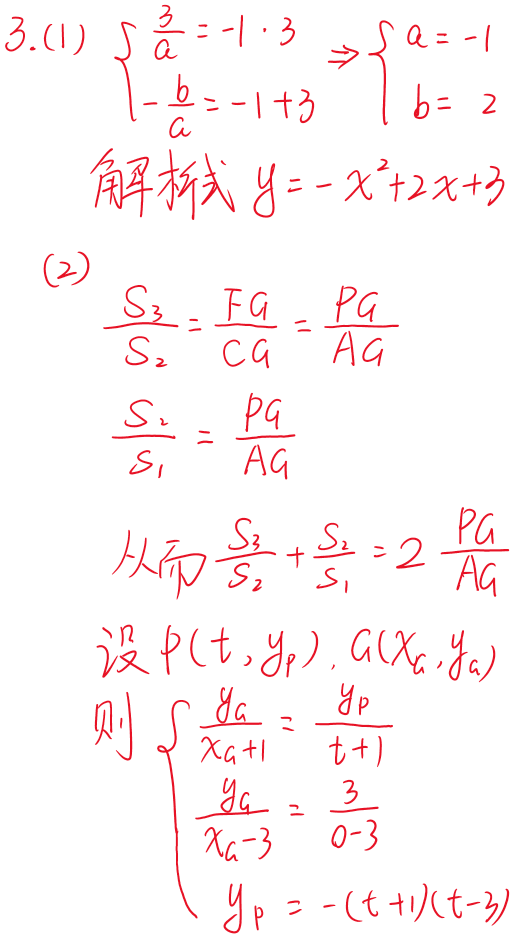
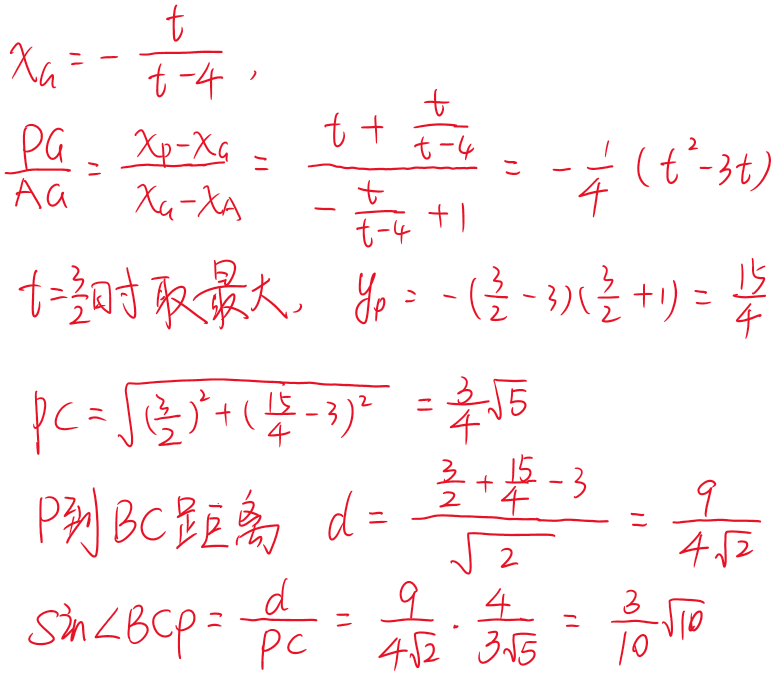
 可以更快获取解答
可以更快获取解答