问题1774: 解三角形

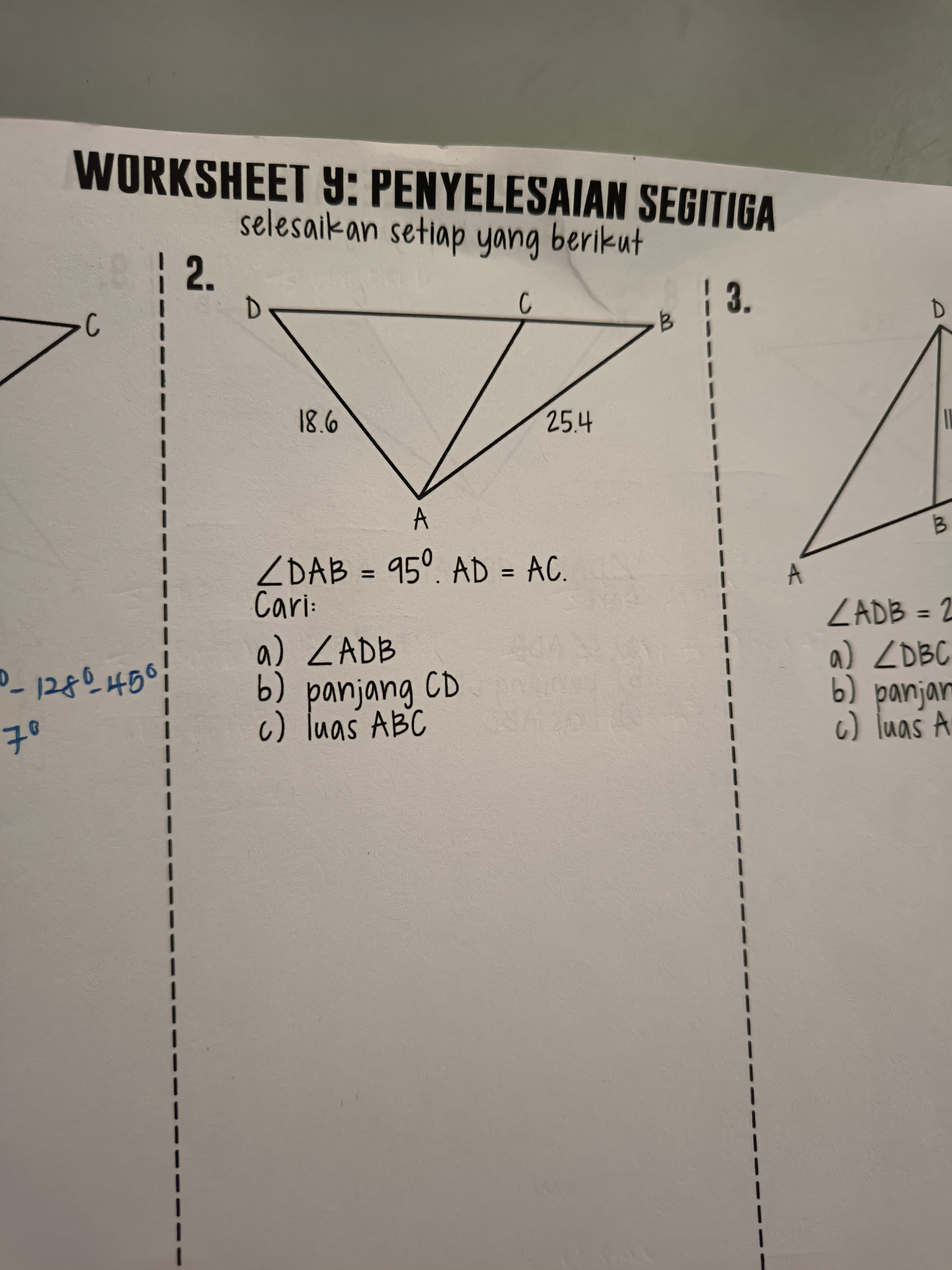
已知：
\( AD = AC = 18.6 \)，\( AB = 25.4 \)，\( \angle DAB = 95^\circ \)，点 \( C \) 在 \( BD \) 上。

(1) 求 \( \angle ADB \)（记为 \( \theta \)）

在 \( \triangle ABD \) 中，用余弦定理求 \( BD \)：
\[
BD^2 = AD^2 + AB^2 - 2 \cdot AD \cdot AB \cdot \cos(95^\circ)
\]
计算：
\( \cos(95^\circ) \approx -0.0872 \)
\[
BD^2 = 18.6^2 + 25.4^2 - 2 \cdot 18.6 \cdot 25.4 \cdot (-0.0872) \approx 345.96 + 645.16 + 82.4 = 1073.52
\]
\[
BD \approx \sqrt{1073.52} \approx 32.77
\]
用正弦定理：
\[
\frac{AB}{\sin \theta} = \frac{BD}{\sin(95^\circ)} \implies \sin \theta = \frac{AB \cdot \sin(95^\circ)}{BD} \approx \frac{25.4 \cdot 0.9962}{32.77} \approx 0.772
\]
\[
\theta = \arcsin(0.772) \approx 50.5^\circ
\]
答： \(\angle ADB \approx 50.5^\circ\)

(2) 求 \( CD \) 的长度

在等腰 \( \triangle ADC \) 中，\( AD = AC = 18.6 \)，\( \angle ADC = \theta \approx 50.5^\circ \)，
\( \angle DAC = 180^\circ - 2\theta \approx 79^\circ \)。
用正弦定理：
\[
\frac{CD}{\sin(\angle DAC)} = \frac{AD}{\sin(\theta)} \implies CD = \frac{AD \cdot \sin(79^\circ)}{\sin(50.5^\circ)} \approx \frac{18.6 \cdot 0.9816}{0.771} \approx 23.7
\]
答： \( CD \approx 23.7 \)

(3) 求 \( \angle ABC \)

在 \( \triangle ABD \) 中：
\[
\angle ABD = 180^\circ - 95^\circ - 50.5^\circ = 34.5^\circ
\]
由于 \( C \) 在 \( BD \) 上，\( \angle ABC = \angle ABD \)。
答： \(\angle ABC \approx 34.5^\circ\)

最终答案：

\[
\boxed{50.5^\circ} \quad \boxed{23.7} \quad \boxed{34.5^\circ}
\]

添加微信可以更快获取解答