问题633: 已知 △ABC 为等腰直角三角形, 其中 AC=BC , 点 P 为边 BC 上一点 (不含点 B,C) , 延长 PC 至 Q , 使得 PC=CQ

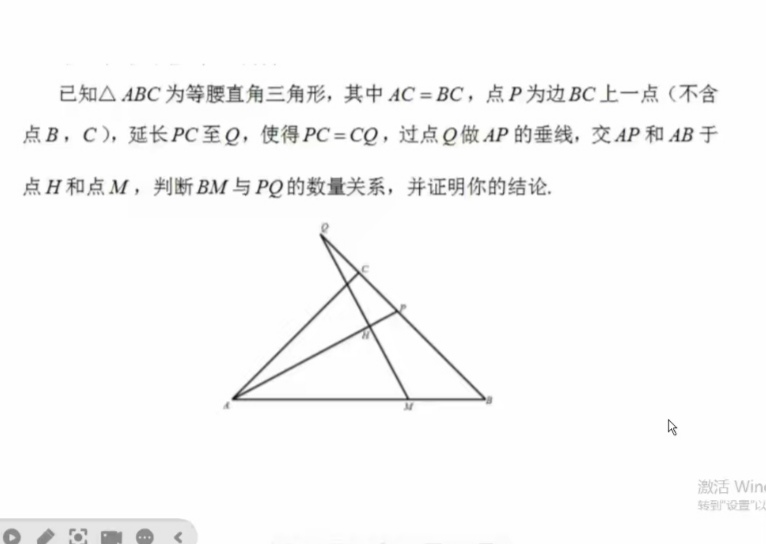
已知 $\triangle A B C$ 为等腰直角三角形, 其中 $A C=B C$, 点 $P$ 为边 $B C$ 上一点 (不含点 $B, C)$, 延长 $P C$ 至 $Q$, 使得 $P C=C Q$, 过点 $Q$ 做 $A P$ 的垂线, 交 $A P$ 和 $A B$ 于点 $H$ 和点 $M$, 判断 $B M$ 与 $P Q$ 的数量关系, 并证明你的结论.