问题750: 重极限

极限问题重述

求二重极限：
\[
\lim_{\substack{x \to 0 \ y \to 0}} \frac{\sin x}{\sqrt{xy + 1} - 1}
\]

初步分析

1. 极限类型：

   • 当 \(x \to 0\) 且 \(y \to 0\) 时：

     • 分子 \(\sin x \to 0\)，
     • 分母 \(\sqrt{xy + 1} - 1 \to 0\)，
   • 因此是 \(\frac{0}{0}\) 型未定式。

2. 方法选择：

   • 可以使用 等价无穷小替换 或 泰勒展开 来简化计算。
   • 这里选择等价无穷小替换，因为形式简单。

步骤详解

第一步：处理分子

当 \(x \to 0\) 时，\(\sin x\) 的等价无穷小为 \(x\)：
\[
\sin x \sim x
\]

第二步：处理分母

分母为 \(\sqrt{xy + 1} - 1\)，可以使用以下技巧：

1. 有理化：
   \[
   \sqrt{xy + 1} - 1 = \frac{(\sqrt{xy + 1} - 1)(\sqrt{xy + 1} + 1)}{\sqrt{xy + 1} + 1} = \frac{xy}{\sqrt{xy + 1} + 1}
   \]
   当 \(xy \to 0\) 时，\(\sqrt{xy + 1} + 1 \to 2\)，因此：
   \[
   \sqrt{xy + 1} - 1 \sim \frac{xy}{2}
   \]
2. 等价无穷小替换：
   也可以直接使用泰勒展开（或二项式近似）：
   \[
   \sqrt{xy + 1} - 1 \approx \frac{xy}{2} + o(xy)
   \]
   因此，主要部分为 \(\frac{xy}{2}\)。

第三步：代入简化

将分子和分母的等价无穷小代入原极限：
\[
\lim_{\substack{x \to 0 \ y \to 0}} \frac{\sin x}{\sqrt{xy + 1} - 1} = \lim_{\substack{x \to 0 \ y \to 0}} \frac{x}{\frac{xy}{2}} = \lim_{\substack{x \to 0 \ y \to 0}} \frac{2}{y}
\]

第四步：极限的存在性

观察简化后的极限：
\[
\lim_{\substack{x \to 0 \ y \to 0}} \frac{2}{y}
\]

• 如果 \(y\) 以任意方式趋近于 0（例如 \(y = kx\) 或 \(y = x^2\)），\(\frac{2}{y}\) 的值会趋向于无穷大或振荡，具体取决于 \(y\) 的趋近方式。
• 因此，该极限 不存在。

验证路径极限

为了进一步验证极限不存在，可以考察不同的趋近路径：

1. 路径 1：令 \(y = x\)，则：
   \[
   \lim_{x \to 0} \frac{\sin x}{\sqrt{x^2 + 1} - 1} = \lim_{x \to 0} \frac{x}{\frac{x^2}{2}} = \lim_{x \to 0} \frac{2}{x} = \infty
   \]
2. 路径 2：令 \(y = x^2\)，则：
   \[
   \lim_{x \to 0} \frac{\sin x}{\sqrt{x^3 + 1} - 1} = \lim_{x \to 0} \frac{x}{\frac{x^3}{2}} = \lim_{x \to 0} \frac{2}{x^2} = +\infty
   \]
3. 路径 3：令 \(y = 0\)，则：
   \[
   \lim_{x \to 0} \frac{\sin x}{\sqrt{0 + 1} - 1} = \lim_{x \to 0} \frac{\sin x}{0}
   \]
   分母为 0，分子为 \(\sin x \to 0\)，但极限不存在（因为分母恒为 0）。

由于不同路径下极限行为不一致（或趋向无穷），原二重极限 不存在。

最终结论

\[
\boxed{\text{该二重极限不存在}}
\]

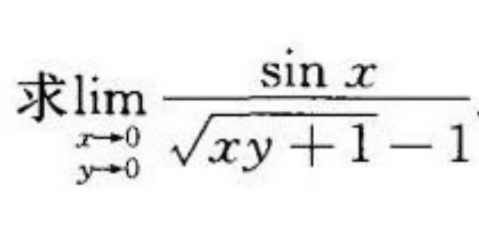
添加微信可以更快获取解答