问题977: 积分计算第一类换元法

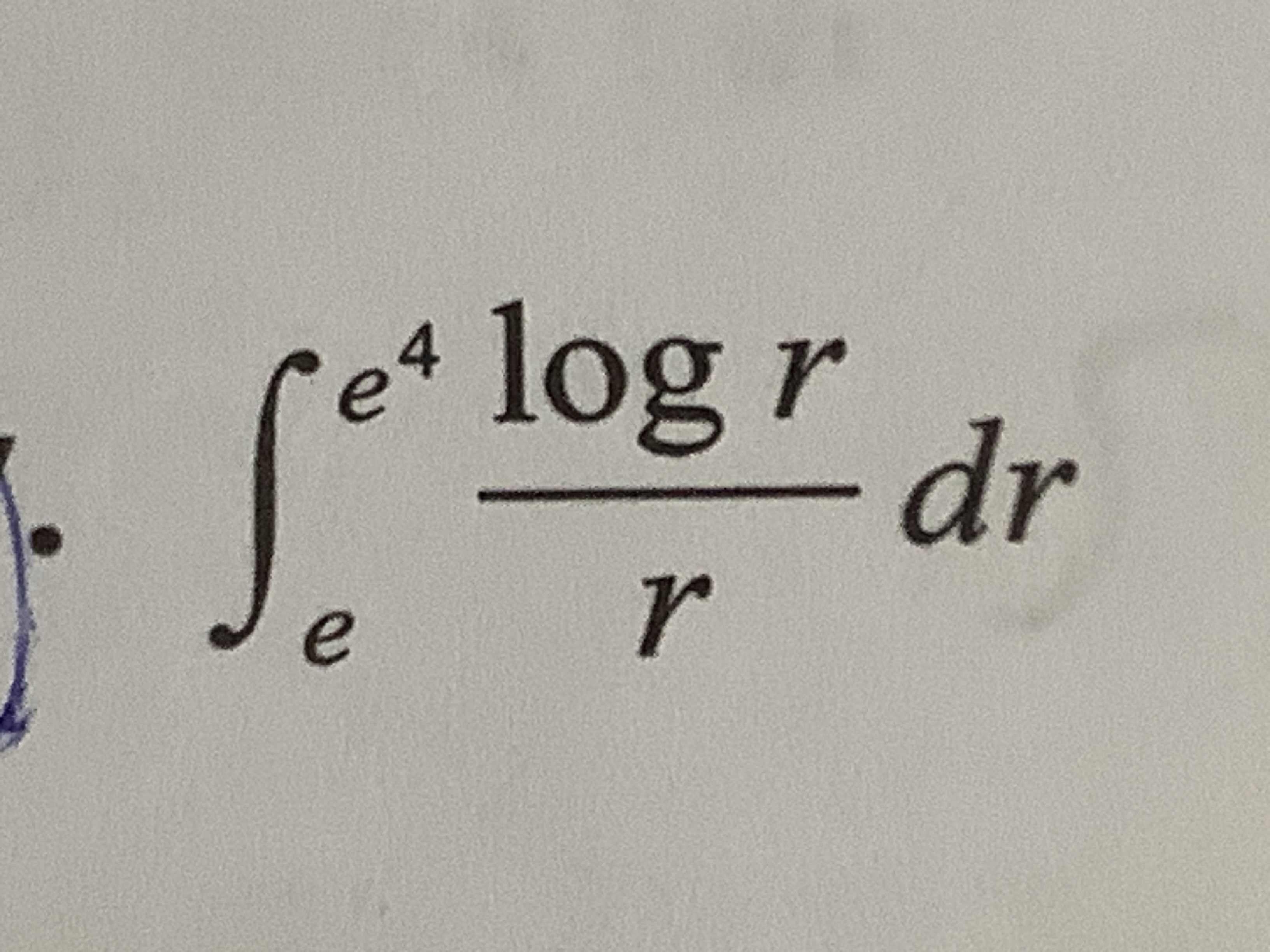
解：

令 \( u = \ln r \)，则 \( du = \frac{1}{r} dr \)。
积分限：\( r = e \Rightarrow u = 1 \)，\( r = e^4 \Rightarrow u = 4 \)。

\[
\int_{e}^{e^4} \frac{\ln r}{r} dr = \int_{1}^{4} u du = \left[ \frac{u^2}{2} \right]_{1}^{4} = \frac{16}{2} - \frac{1}{2} = \frac{15}{2}
\]

\[
\boxed{\frac{15}{2}}
\]

添加微信可以更快获取解答