问题111: 一架小飞机有 4 排座位，每排有 3 个座位。已经有八名乘客登机，他们在这些座位中随机就坐.

分析

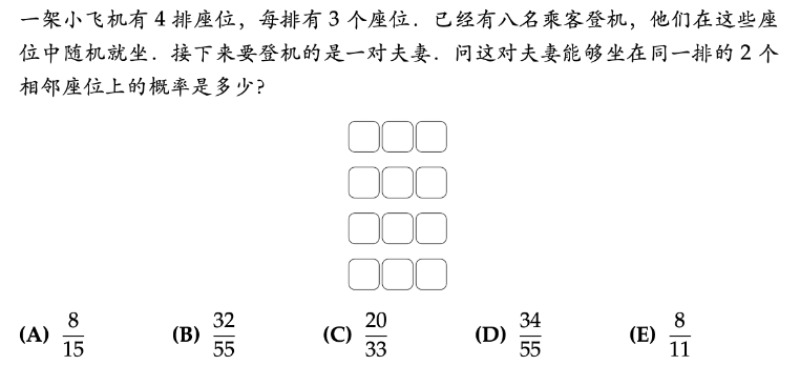
由于座位总数是12个, 因此当8名乘客登机后, 还剩下4个空座. 夫妻能坐在同一排相邻座位的概率就是四个空座至少有一对空座相邻的概率.
因此问题转化为: 12个座位中任选4个, 至少有一对座位相邻的概率. 这样就有了以下两种思路:

• 思路一: 直接分情况计数四个座位中至少一对座位相邻的情形
• 思路二: 先分情况计数四个座位全部不相邻的情形, 然后用总数减去全部不相邻的情形数, 就是至少有一对座位相邻的情形.
  按照这两个思路, 就有了以下两种方法.

方法一

总共四个空座, 四个空座有两个相邻的情形共四种:

• 情形一：某一排3个，另一排1个，共 $C_4^3 \cdot C_9^1=36$ 种.
• 情形二：某一排相邻2个，另2排各1个，共 $C_4^3 \cdot C_2^1 \cdot C_3^2 \cdot 3 \cdot 3=216$ 种
• 情形三: 某一棑相邻 2 个，另一排不相邻2个, 共 $C_4^1 \cdot C_2^1 \cdot C_3^1=24$ 种
• 情形四: 某二排相邻 2 个，共 $C_4^2 \cdot C_2^1 \cdot C_2^1=24$ 种

如图所示:

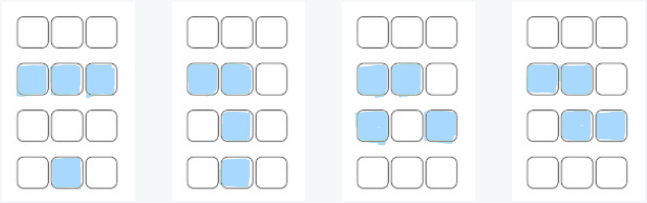
从而所求概率为

$$\frac{36+216+24+24}{C_{12}^4}=\frac{20}{33}$$

方法二

总共四个空座, 它们都不相邻的情形有三种:

• 情形一: 每排一个空座, 共$3^4=81$种
• 情形二: 某一排有不相邻的两个空座, 另外两排各一个空座, 共$C_4^1 \cdot C_3^2 \cdot 3^2=108$种
• 情形三: 某两排各有不相邻的两个空座, 共$C_4^2=6$种

三种情形如图所示:

12个座位中任选4个的情形数是$C_{12}^4=495$种, 从而至少一对空座相邻的概率是
$$\frac{C_{12}^4 - 81 - 108 - 6}{C_{12}^4}= \frac{300}{495} = \frac{20}{33}$$

添加微信可以更快获取解答（请注明有偿答疑）