问题1566:

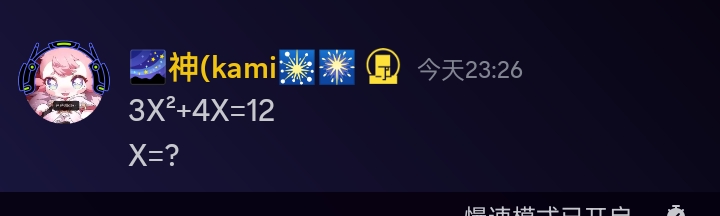
本题可通过一元二次方程的求根公式来求解\(x\)的值。

步骤一：将方程化为一元二次方程的一般形式

一元二次方程的一般形式为\(ax^2 + bx + c = 0\)（\(a\neq0\)）。
对于方程\(3x^2 + 4x = 12\)，移项可得\(3x^2 + 4x - 12 = 0\)，其中\(a = 3\)，\(b = 4\)，\(c = -12\)。

步骤二：计算判别式\(\Delta=b^2 - 4ac\)的值

将\(a = 3\)，\(b = 4\)，\(c = -12\)代入判别式\(\Delta=b^2 - 4ac\)中，可得：
\(\Delta = 4^2 - 4\times3\times(-12)\)
\(= 16 + 144\)
\(= 160\)

步骤三：代入求根公式求解\(x\)的值

一元二次方程\(ax^2 + bx + c = 0\)（\(a\neq0\)）的求根公式为\(x = \frac{-b\pm\sqrt{\Delta}}{2a}\)。
将\(a = 3\)，\(b = 4\)，\(\Delta = 160\)代入求根公式可得：
\(x = \frac{-4\pm\sqrt{160}}{2\times3}=\frac{-4\pm4\sqrt{10}}{6}=\frac{-2\pm2\sqrt{10}}{3}\)
即\(x_1 = \frac{-2 + 2\sqrt{10}}{3}\)，\(x_2 = \frac{-2 - 2\sqrt{10}}{3}\)。

综上，\(x\)的值为\(\frac{-2 + 2\sqrt{10}}{3}\)或\(\frac{-2 - 2\sqrt{10}}{3}\)。

添加微信可以更快获取解答