问题1785: 有理函数积分计算

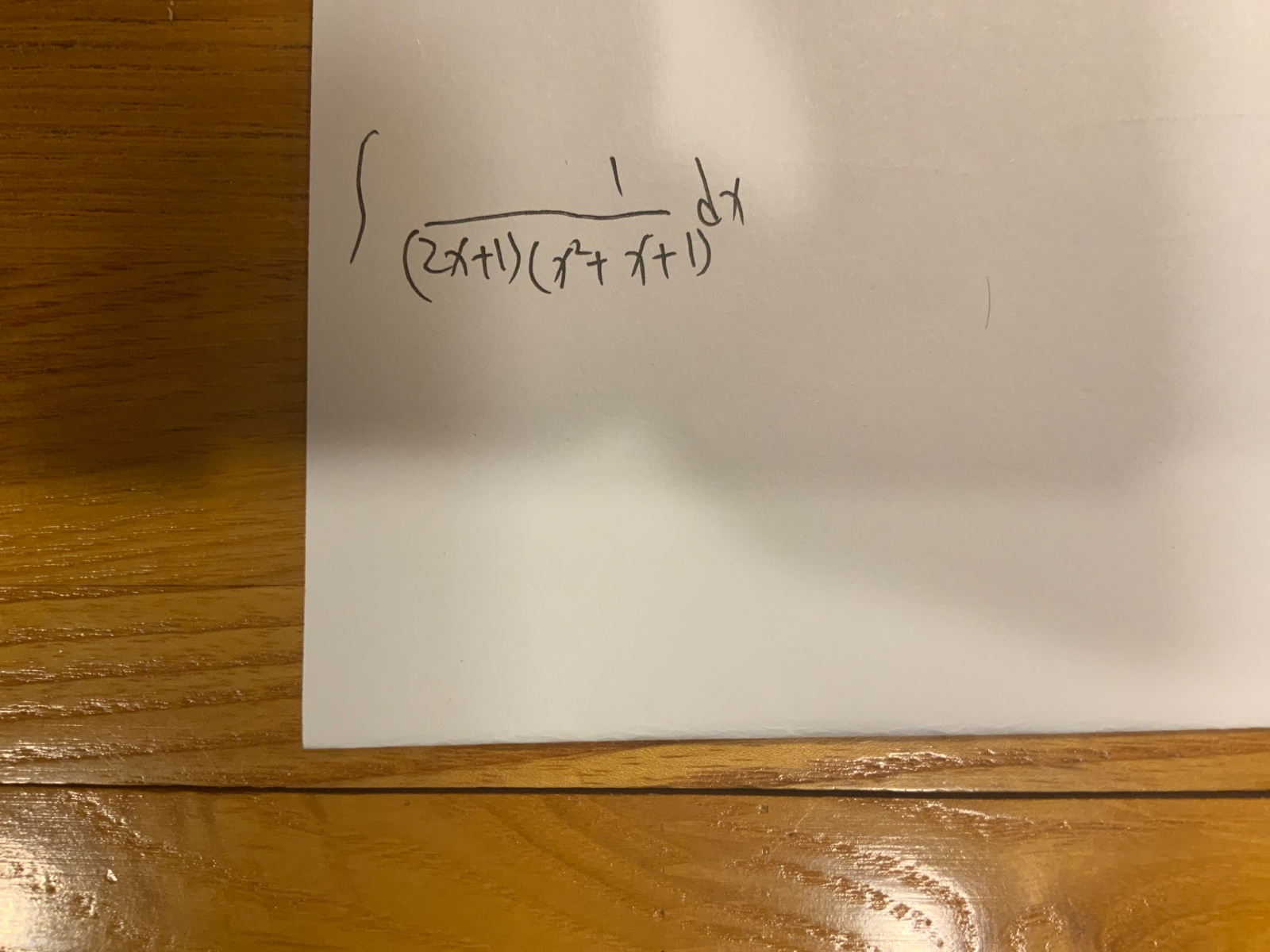
解：

\[
I = \int \frac{1}{(2x + 1)(x^2 + x + 1)} \, dx
\]

一、部分分式分解

设：
\[
\frac{1}{(2x + 1)(x^2 + x + 1)} = \frac{A}{2x + 1} + \frac{Bx + C}{x^2 + x + 1}
\]
通分后比较系数，解得：
\[
A = \frac{4}{3}, \quad B = -\frac{2}{3}, \quad C = -\frac{1}{3}
\]
即：
\[
\frac{1}{(2x + 1)(x^2 + x + 1)} = \frac{4}{3(2x + 1)} - \frac{2x + 1}{3(x^2 + x + 1)}
\]

二、积分化简

\[
I = \frac{1}{3} \int \frac{4}{2x + 1} \, dx - \frac{1}{3} \int \frac{2x + 1}{x^2 + x + 1} \, dx
\]

三、计算积分

1. \(\int \frac{4}{2x + 1} \, dx = 2 \ln|2x + 1|\)
2. \(\int \frac{2x + 1}{x^2 + x + 1} \, dx = \ln(x^2 + x + 1)\)（∵分子为分母的导数）

四、最终结果

\[
I = \frac{2}{3} \ln|2x + 1| - \frac{1}{3} \ln(x^2 + x + 1) + C
\]

或合并为：
\[
\boxed{\frac{1}{3} \ln \left| \frac{(2x+1)^2}{x^2 + x + 1} \right| + C}
\]

添加微信可以更快获取解答