问题241: 如图，AFE，BGF，CHG，DEH分别共线， BG=AF=DE=CH, 四边形 ABCD 为正方形. 求证: 四边形EFGH为正方形
如图，AFE，BGF，CHG，DEH分别共线， $B G=A F=D E=C H$, 四边形 $A B C D$ 为正方形. 求证: 四边形EFGH为正方形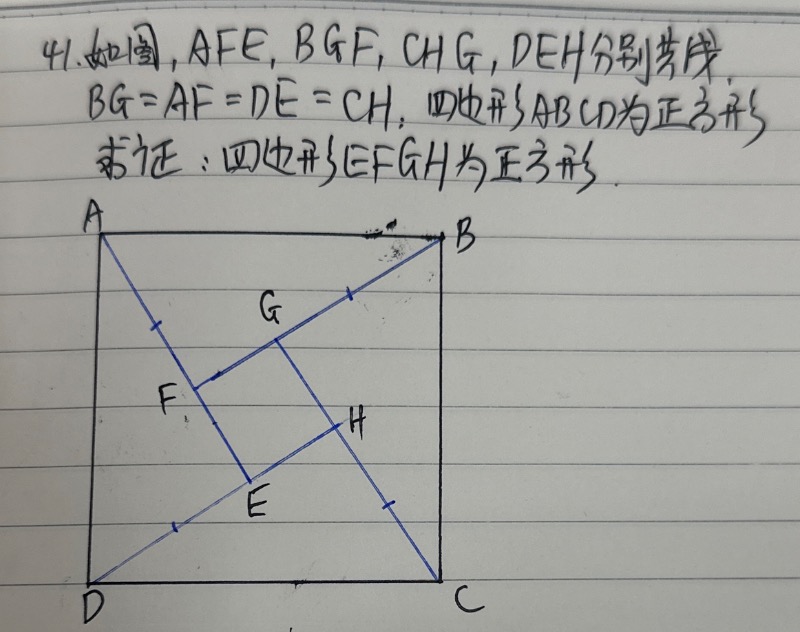
问题
解答
等待解答
添加微信
可以更快获取解答（请注明有偿答疑）
最后修改于3月29日
添加新讨论
提交新的问题
前一篇：问题239: 求解以下方程
下一篇：问题242: 康能健身院在十月份的盈利是九月份的2倍，十一月份的盈利则是十月份的3倍．这3个月的总盈利是RM 160335。计算十月份的盈利。
先根据互补得出直角，证得中间为矩形。再用边角边证四个三角形全等，可得四个三角形的长直角边相等，长直角边减去短直角边，可得矩形的四边都相等。四边都相等的矩形是正方形，得证。