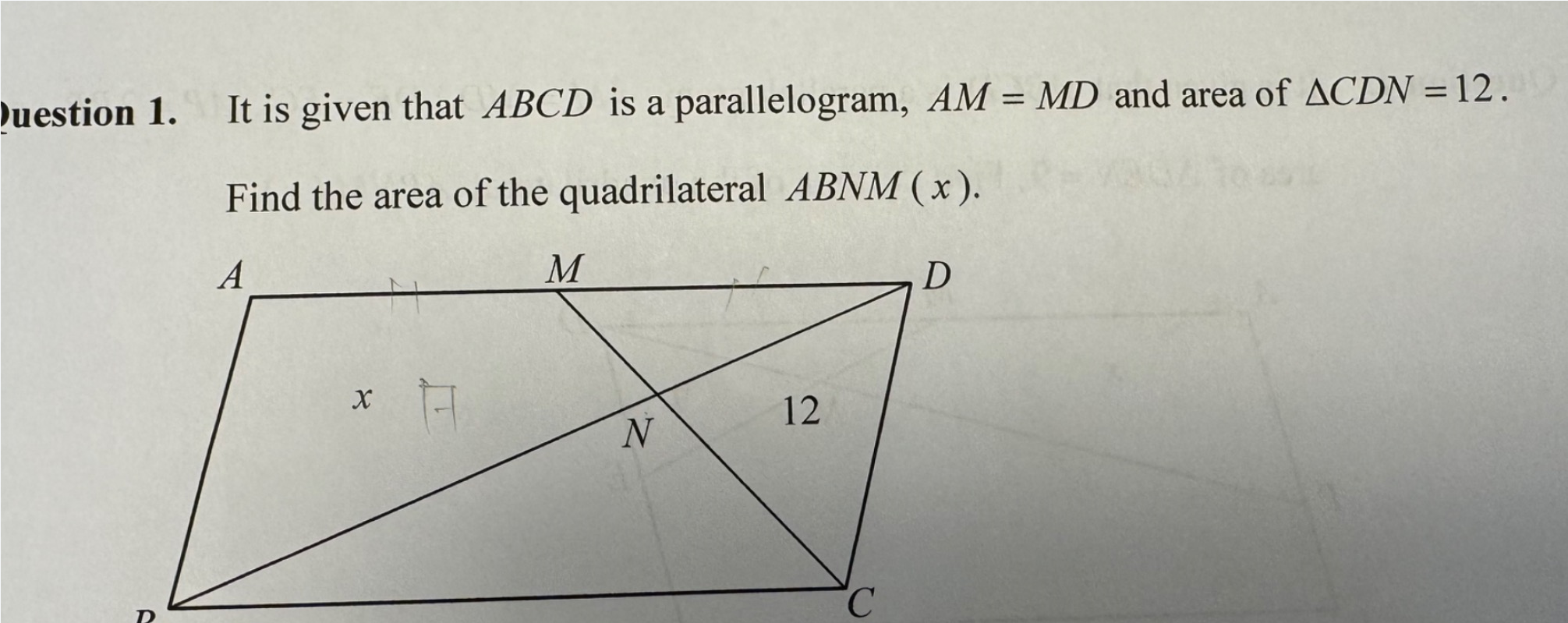
问题157: It is given that ABCD is a parallelogram, AM=MD and area of △CDN=12 . Find the area of the quadrilateral ABNM(x) .
It is given that $A B C D$ is a parallelogram, $A M=M D$ and area of $\triangle C D N=12$. Find the area of the quadrilateral $A B N M(x)$.
已解决 · 初中数学
三角形相似
提问于2024年02月27日 · 阅读 1084
$$
\begin{aligned}
& \because \angle M N D=\angle C N B, \angle M D N=\angle C B N \therefore \triangle M N D \backsim \triangle C N B \\
& \because M \text { 是中点 } \therefore M D: A D=M D: C B=1: 2 \\
& \therefore M N: C N=M D: C B=1: 2 \\
& \because \triangle M N D \text { 与 } \triangle C N D \text { 等高且底边 } M N: C N=1: 2 \\
& \therefore S_{\triangle M N D}: S_{\triangle C N D}=1: 2 \\
& \therefore S_{\triangle M N D}=\frac{1}{2} S_{\triangle C N D}=\frac{1}{2} \cdot 12=6 \\
& \because S_{\triangle B N C}=\left(\frac{B C}{D M}\right)^2 \cdot S_{\triangle M N D}=2^2 \cdot 6=24 \\
& \therefore S_{\triangle C B D}=S_{\triangle C B N}+S_{\triangle C D N}=24+12=36 \\
& \therefore S_{\triangle A B D}=S_{\triangle C B D}=36 \\
& \therefore S_{A B N M}=S_{\triangle A B D}-S_{\triangle M N D}=36-6=30
\end{aligned}
$$
添加微信 可以更快获取解答
可以更快获取解答
最后修改于2024年02月28日
前一篇:问题156: {-3[-(-xy)³]²-(-x²y²)³}:(-x²y³)²
下一篇:问题158: 圖中, H 是 AC 上的一點, 使得 BH 是 △ABC 的一條高線。若 AB=AC 及 ∠BAC=40 , 求 ∠CBH 。
相关文章
问题169: 已知正方形 ABCD 边长为 40,E 点为 BC 边上一点, 其中 DE=EF,DE⊥EF,FD 与 AB 交于且 AG=10 , 求 △FED 的面积。
问题112: In the figure, prove that △ABC∼△AED .

 可以更快获取解答
可以更快获取解答