问题412: 如图,△ABC中,∠BAC=60°,D、E分别是边BC、边AC上点,满足∠CDE=2∠BAD,DA=DC,若 BD=1,ED=2,则 AB的长为多少?

老师不会写
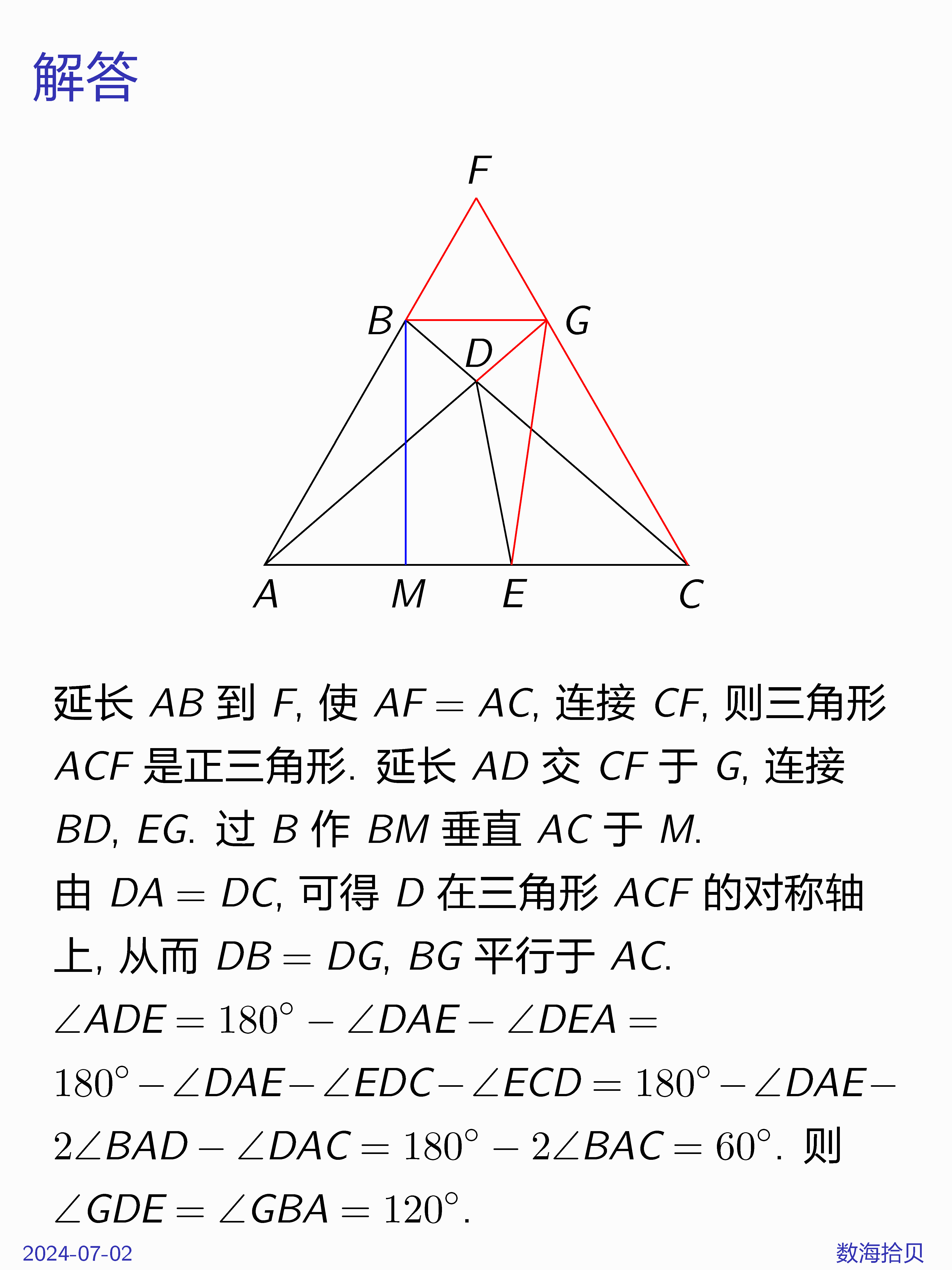
如图,△ABC中,∠BAC=60°,D、E分别是边BC、边AC上点,满足∠CDE=2∠BAD,DA=DC,若
BD=1,ED=2,则 AB的长为多少?

添加微信 可以更快获取解答
可以更快获取解答
最后修改于2024年07月02日
前一篇:问题411: 定积分计算
下一篇:问题413: Mr Lam plans to invest $50000 for 10 years. He may buy a gov
这个几何题的目的是要找到三角形 \(ABC\) 中 \(AB\) 的长度。首先,让我们总结一下给出的信息:
\( \angle BAC = 60^\circ \)\( D \) 和 \( E \) 分别是 \( BC \) 的内点,且 \( DA = DC \), \( \angle CDE = \angle BAD \).\( BD = 1 \), \( DE = 2 \).要求计算 \( AB \) 的长度。我们可以使用以下步骤来解题:
步骤 1:利用角度信息由于 \( \angle BAC = 60^\circ \) 且 \( D \) 在 \( BC \) 上使得 \( DA = DC \),则 \( D \) 是 \( BC \) 的中点。因此,\( D \) 到 \( B \) 和 \( C \) 的距离相等。
步骤 2:利用线段长度信息已知 \( BD = 1 \) 且 \( DE = 2 \),且 \( D \) 是 \( BC \) 的中点,所以 \( DC = DB = 1 \)。
步骤 3:构建三角形和计算由于 \( D \) 是 \( BC \) 的中点,那么 \( BC = BD + DC = 1 + 1 = 2 \)。
现在,我们已经知道 \( \triangle ABC \) 是一个角 \( BAC \) 为 \( 60^\circ \) 的等腰三角形(因为 \( \angle BAC = 60^\circ \),且 \( DA = DC \) 暗示 \( D \) 在 \( BC \) 的中点),我们可以得出 \( AB = AC \)。使用等腰三角形的性质和 \( BC \) 的长度计算 \( AB \)。
步骤 4:使用余弦定律或三角形的特性对于等腰三角形 \( \triangle ABC \),其中 \( \angle BAC = 60^\circ \) 且 \( BC = 2 \),\( AB \) 的长度可以通过余弦定律来计算:
$$ c^2 = a^2 + b^2 - 2ab \cos C $$
将 \( a = b = AB \), \( C = 60^\circ \), \( c = 2 \) 代入,得:
$$ 2^2 = AB^2 + AB^2 - 2 \cdot AB \cdot AB \cdot \frac{1}{2} $$
简化后:
$$ 4 = 2AB^2 - AB^2 $$
$$ AB^2 = 4 $$
$$ AB = 2 $$
因此,\( AB \) 的长度为 2。