问题1558:
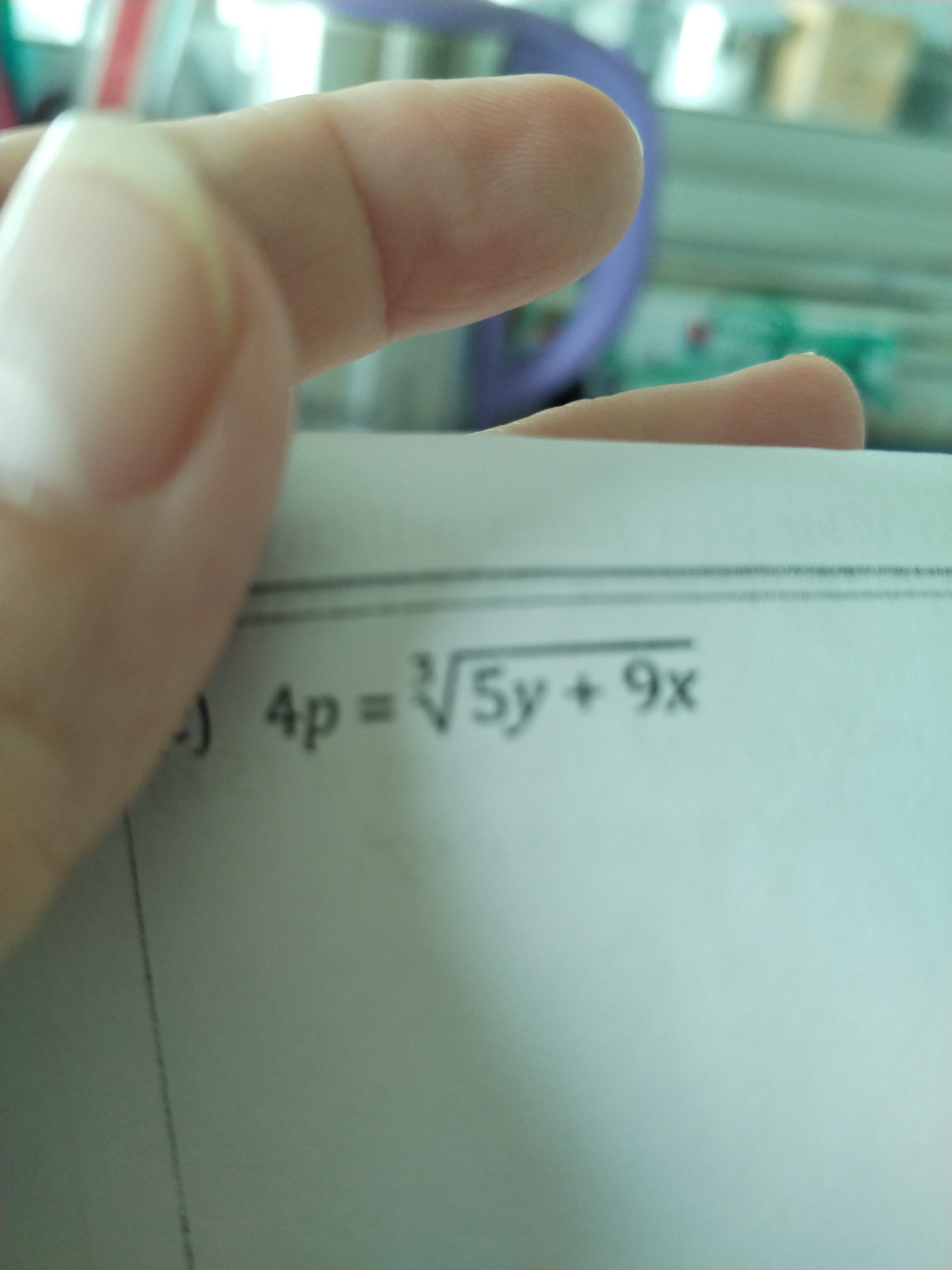
已解决
提问于2025年04月09日 · 阅读 735
本题可对给定方程进行变形求解,以下为详细过程:
已知方程\(4p = \sqrt[3]{5y + 9x}\),若要求用其他变量表示某一变量,可根据根式运算的性质进行变形。
综上,若求\(p\),则\(p=\frac{1}{4}\sqrt[3]{5y + 9x}\);若求\(5y + 9x\),则\(5y + 9x = 64p^3\);若求\(y\),则\(y=\frac{64p^3 - 9x}{5}\)。
添加微信 可以更快获取解答
可以更快获取解答
最后修改于2025年04月16日
前一篇:问题1557:
下一篇:问题1559: