已知点P(x, y)的坐标满足, 则x+y/√(x^2+y^2)的取值范围为

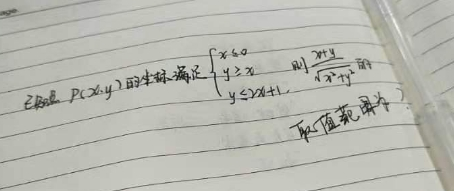
$$ \begin{aligned} \frac{x+y}{\sqrt{x^2+y^2}} & =\frac{x}{\sqrt{x^2+y^2}}+\frac{y}{\sqrt{x^2+y^2}} \\ & =\cos \theta+\sin \theta \\ & =\sqrt{2} \sin \left(\theta+\frac{\pi}{4}\right) \end{aligned} $$

下求$\theta$的范围即可

根据题意画出点$(x, y)$的范围

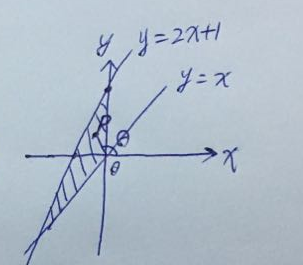
可以看到$\frac{\pi}{2} \leqslant \theta \leqslant \frac{5}{4} \pi$,
从而 $\frac{3}{4} \pi \leqslant \theta+\frac{\pi}{4} \leqslant \frac{3}{2} \pi$
又$\sqrt{2} \sin \left(\theta+\frac{\pi}{4}\right)$ 在 $\left[\frac{\pi}{2}, \frac{5}{4} \pi\right]$单调递减, 从而取值范围是$[-1, \sqrt{2}]$

添加微信可以直接提问（请注明数学答疑）

最后修改于2023年05月20日