问题93: 反三角函数有哪些性质?

图形

基本公式

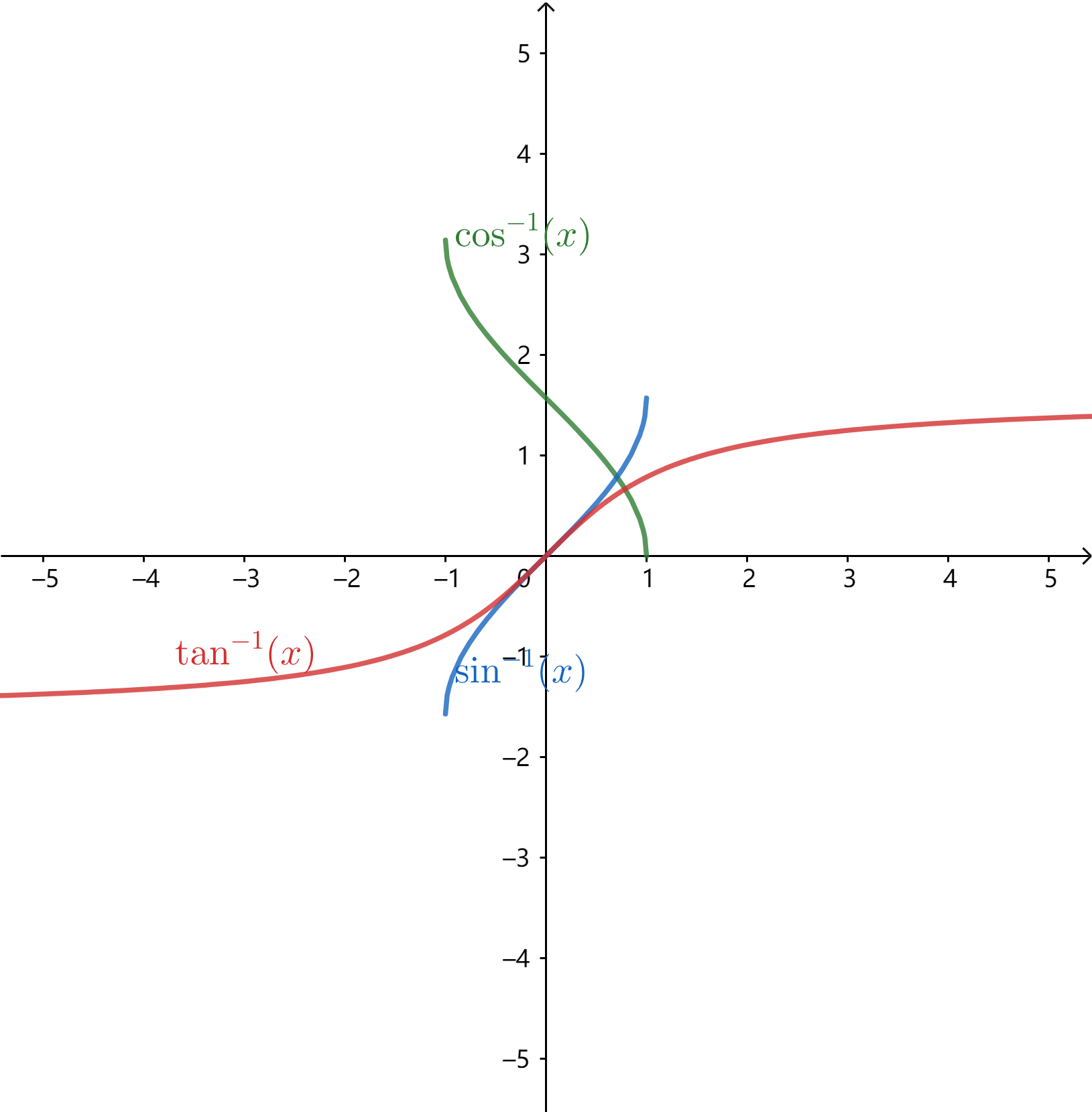
$$ \begin{aligned} & \arccos x=\frac{\pi}{2}-\arcsin x \\ & \operatorname{arccot} x=\frac{\pi}{2}-\arctan x \\ & \operatorname{arccsc} x=\frac{\pi}{2}-\operatorname{arcsec} x \end{aligned} $$

倒数关系

$$ \begin{aligned} \arccos \left(\frac{1}{x}\right) & =\operatorname{arcsec}(x) \\ \arcsin \left(\frac{1}{x}\right) & =\operatorname{arcsc}(x) \\ \arctan \left(\frac{1}{x}\right) & =\frac{\pi}{2}-\arctan (x)=\operatorname{arccot}(x), x>0 \\ \arctan \left(\frac{1}{x}\right) & =-\frac{\pi}{2}-\arctan (x)=\operatorname{arccot}(x)-\pi, x<0 \\ \operatorname{arccot}\left(\frac{1}{x}\right) & =\frac{\pi}{2}-\operatorname{arccot}(x)=\arctan (x), x>0 \\ \operatorname{arccot}\left(\frac{1}{x}\right) & =\frac{3 \pi}{2}-\operatorname{arccot}(x)=\pi+\arctan (x), x<0 \\ \operatorname{arcsec}\left(\frac{1}{x}\right) & =\arccos (x) \\ \operatorname{arccsc}\left(\frac{1}{x}\right) & =\arcsin (x) \end{aligned} $$

负数关系

$$ \begin{aligned} & \arcsin (-x)=-\arcsin x \\ & \arcsin (-x)=-\arcsin x \\ & \arccos (-x)=\pi-\arccos x \\ & \operatorname{arccot}(-x)=\pi-\operatorname{arccot} x \\ & \operatorname{arcsec}(-x)=\pi-\operatorname{arcsec} x \\ & \operatorname{arcsec}(-x)=\pi-\operatorname{arcsec} x \\ & \operatorname{arcsec}(-x)=\pi-\operatorname{arcsec} x \\ & \operatorname{arccsc}(-x)=-\operatorname{arccsc} x & \end{aligned} $$

同角关系

$$ \begin{aligned} & \arccos (x)=\arcsin \left(\sqrt{1-x^2}\right), 0 \leq x \leq 1, \\ & \arccos \left(\frac{1-x^2}{1+x^2}\right)=\arcsin \left(\frac{2 x}{1+x^2}\right), 0 \leq x \leq 1 \\ & \arccos (x)=\frac{1}{2} \arccos \left(2 x^2-1\right), 0 \leq x \leq 1 \\ & \arcsin (x)=\frac{1}{2} \arccos \left(1-2 x^2\right), 0 \leq x \leq 1 \\ & \arcsin (x)=\arctan \left(\frac{x}{\sqrt{1-x^2}}\right) \\ & \arctan (x)=\arcsin \left(\frac{x}{\sqrt{1+x^2}}\right) \\ & \operatorname{arccot}(x)=\arccos \left(\frac{x}{\sqrt{1+x^2}}\right) \end{aligned} $$

添加微信可以更快获取解答（请注明有偿答疑）